OnlyBadForecasts

Introduction

I love time-series forecasting. To me it is the holy grail of machine learning, but I pretty much suck at it.

This is an attempt at a long term forecast of snowpack in Utah. Currently, the project is limited to forecasting SWE (snow water equivalent) at Brighton. All of my raw data is sourced from the USDA’s Natural Resources Conservation Service.

Methodology

In depth write-up coming soon-ish…

In the meantime, my methodology is inspired by this paper.

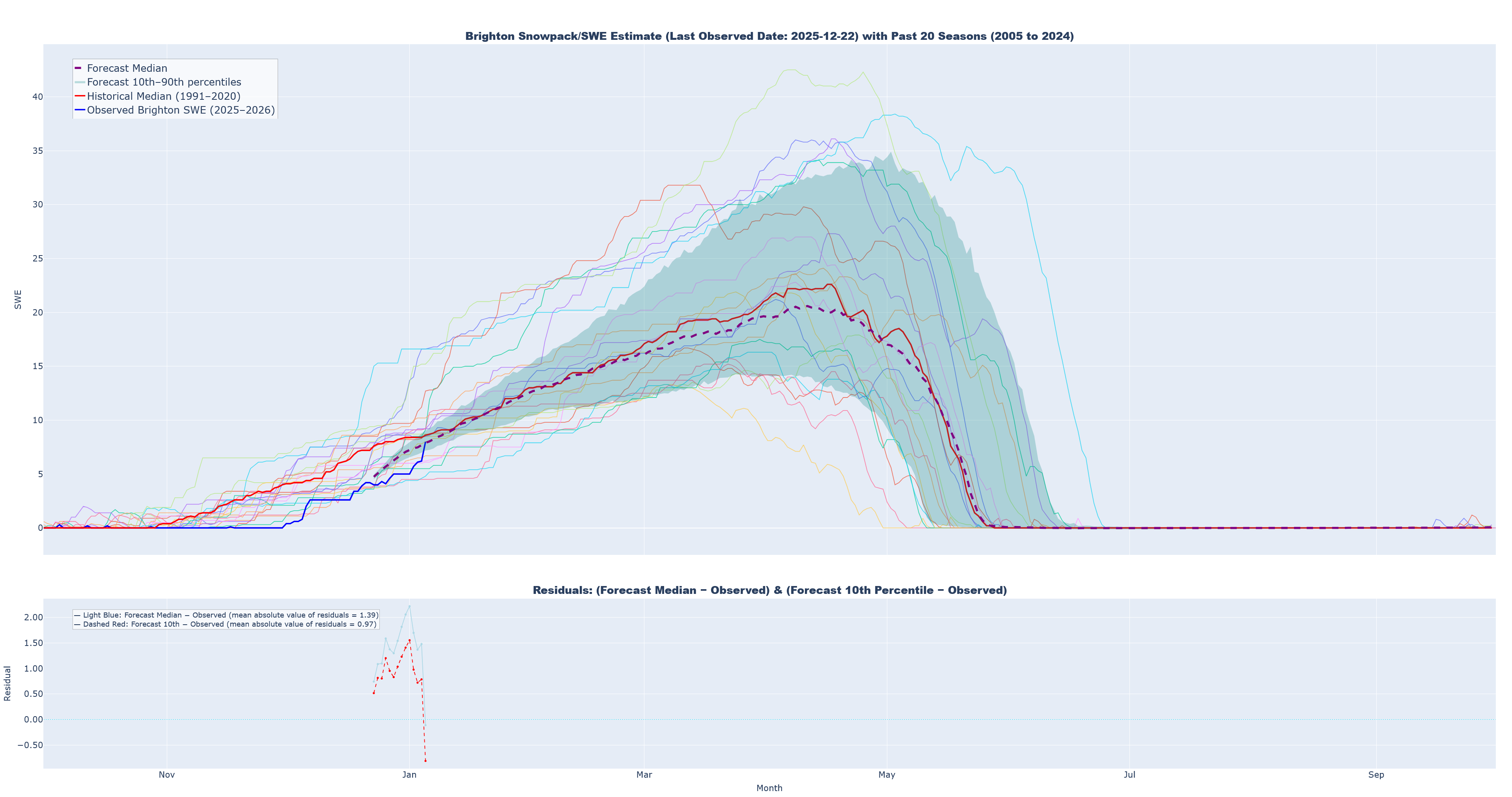
My first attempt broke historical data up into chunks of 60 day windows, 2 cylical features, and a target. Examples were fed into a simple MLP with a single dropout layer. Feed forward prediction was uesed to create 300 futures paths. As per Gal and Ghahramani, I kept dropout layers live to during inference. From these 300 trajectories I calculate a 10th and 90th percentile as well as a median: these figures essentially become my prediction.

Looking at the charts, one thing that is starting to worry me is how similarly prediction curves seem to match with the shape of the historical median. Even without being fed it explicitly, I am worried that the model essentially learned the easiest way to minimize loss was to use the median, and that no matter when in the season or at what value of SWE the prediction starts the model sort of “runs home to mama”. With the recent storm around 2026/01/05, there is a very real possibility that true values will move above the historical median, and I am very interested to see if the model begins predicting down to the median even after this. I also think that maybe the model will just predict the median +/- the last observed value: I will have to build out a way to monitor this.

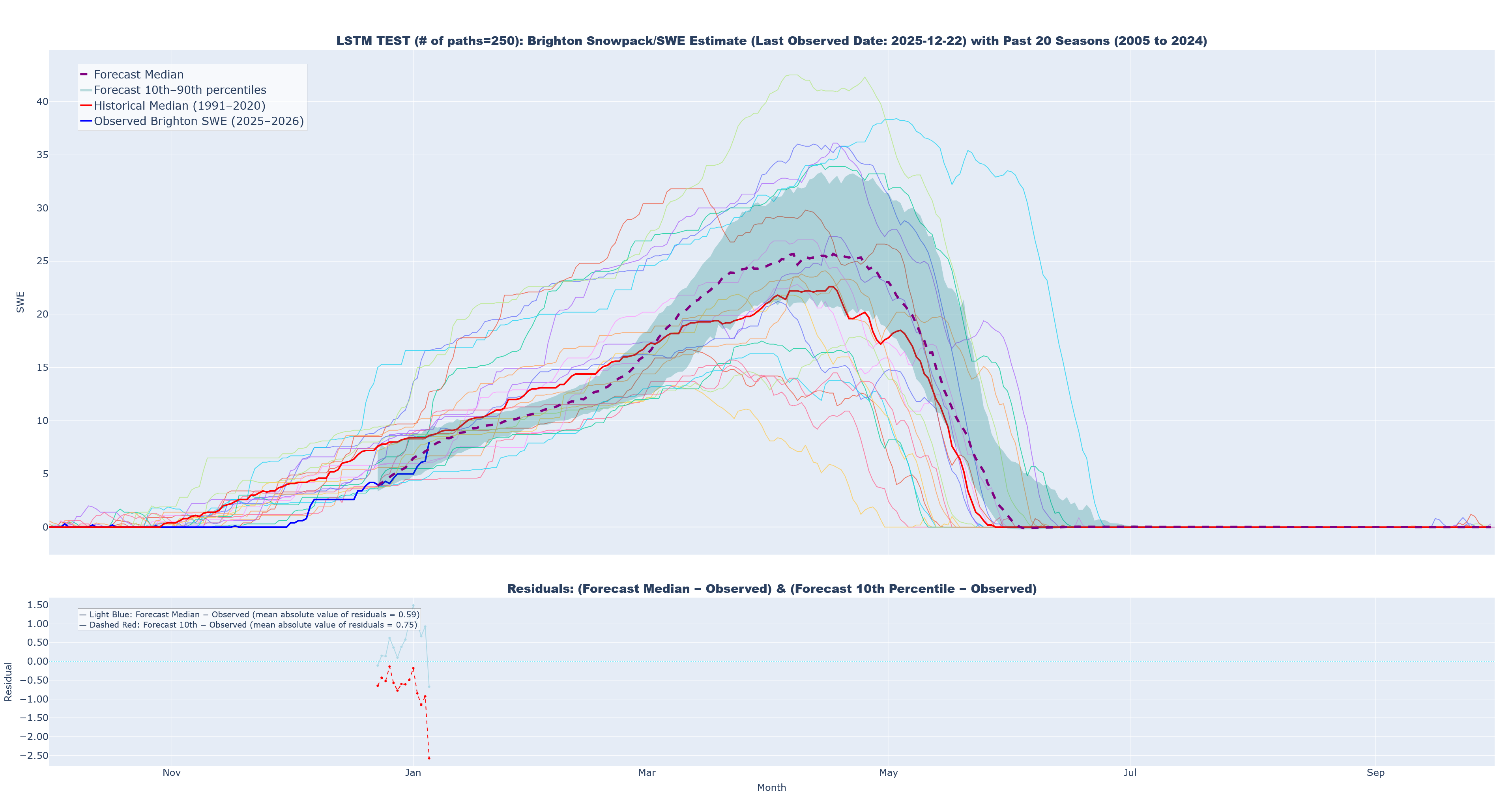
As my first alternative/sensitivity analysis, I created a similar workflow using LSTM layers (To reviewer #3: I am still avoiding auto-regressive options like ARIMA, SARIMA, or SARIMAX). Initial results only used 20 predicted trajectories, as prediction is massively slower. On my machine, the MLP approach takes about 5 minutes to create all 300 paths, but the LSTM approach will likely take 4.5+ hours to complete 300. MY first first runs were limited to 20 paths, but I have since expanded this to 250. Attached below the Notes section is a chart that shows the results when using an LSTM and a prediction that starts at 2025-12-22. To my eye, the most striking differences are related to how much tighter the bastardized confidence interval appears, how little the 10th and 90th percentiles seem to vary in their distance from the median prediction regardless of how far in the future predictions are, and the jagged more inconsistent shape of the entire path. We will see what happens as more data accumulates.

For both approaches, I want to add in a new feature: day distance (positive or negative) from the expected peak day. The raw data contains a marker showing that the median peak day across years is YYYY-04-10. I think the model would benefit from this as it would add in signal about where in the accumulation/peak/melt phase each observation lies, and this might work in concert with the cyclical features to improve performance. I will work on this later, but it should be an easy add. That said, while hopeful, I am already concerned that this feature will artificially create a peak at April, 10th when in reality the peak date can vary widely (I will chart this).

Some of this screed may fit better in the results or conclusions sections, but for the moment it all stays here.

Results

Below are visualizations for each round of prediction. Moving forward, my plan is to update predictions on a weekly cycle starting from 2026-01-04, but if major storms occur I may rerun predictions on an ad-hoc basis. I will save out past predictions and key metrics to gauge their relative accuracy over time.

Current metrics

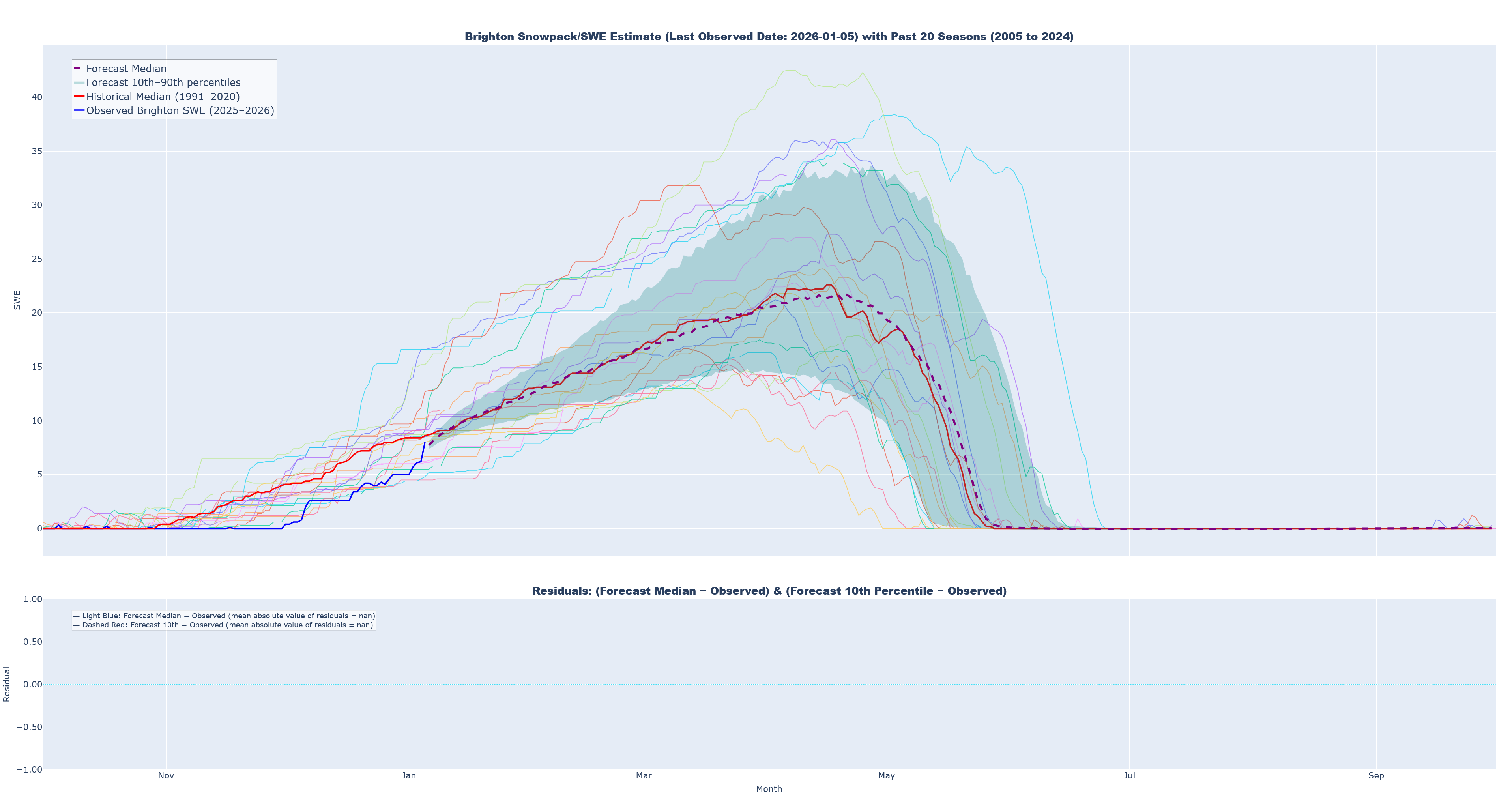
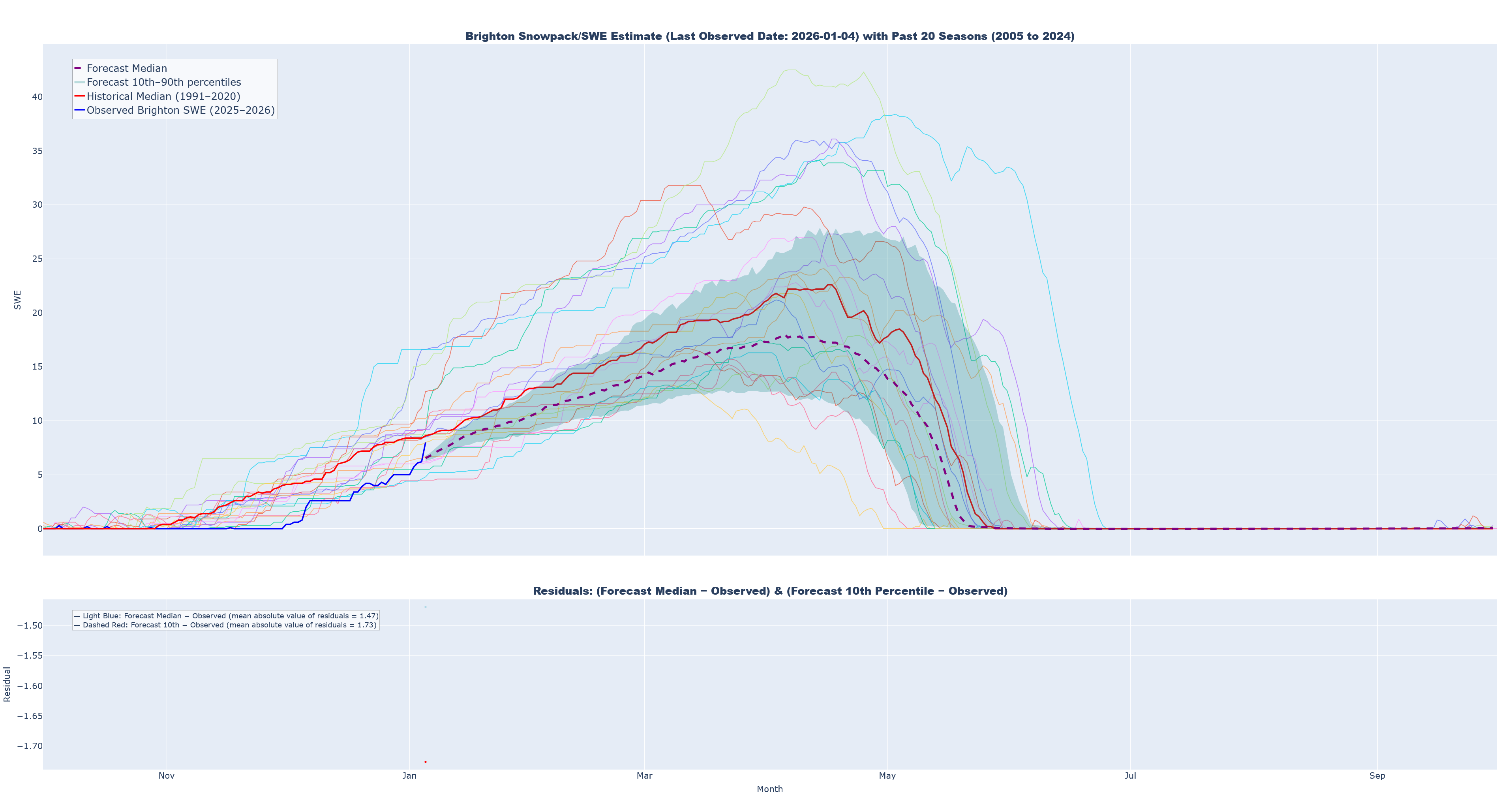
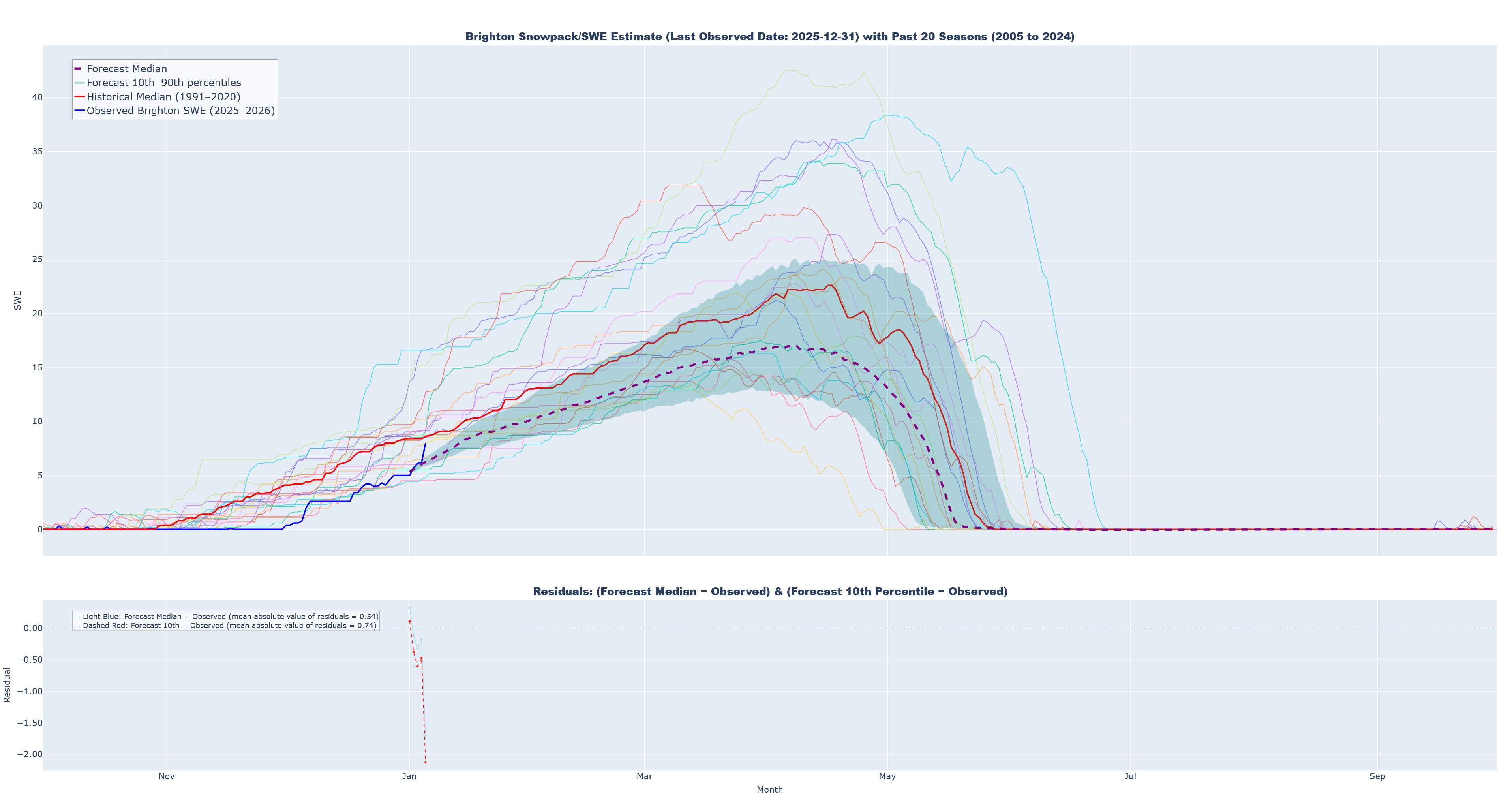
  1. 2025-2026 observed SWE at Brighton (solid blue)
  2. Median simulated SWE (dashed purple)
  3. 10th to 90th percentiles for simulated trajectories (teal band)
  4. 1991-2020 historical median (solid red)
  5. The past 20 seasons of historical data (thin solid lines of various colors)
  6. A secondary chart that quantifies residuals

Median Prediction, Prediction 10th-90th Percentiles, Historical Median (‘91-‘20), Past 20 Seasons, and Residuals

Prediction 4: Last Observed Date: 2026-01-05

2026 01 05 predictions

Prediction 3: Last Observed Date: 2026-01-04

2026 01 04 predictions

Prediction 2: Last Observed Date: 2025-12-31

2025 12 31 predictions

Prediction 1: Last Observed Date: 2025-12-22

2025 12 22 predictions

Notes

LSTM Test (250 predictions) Last Observed Date: 2025-12-22

2025 12 22 predictions